Square Footage Calculator

Square footage calculator

Our versatile square footage calculator is a free online tool designed to quickly compute the surface area of various geometric shapes, including squares, triangles, circles, rectangles, rectangle borders, circle borders, annuluses, and trapezoids. Whether you are a DIY enthusiast or a professional contractor, this tool makes it easy to calculate square footage for the most common shapes used in construction and landscaping.

This area calculator is an essential resource for finding the surface area of a room, yard, or garden, helping you accurately estimate the materials needed for your next project. By factoring in the price per square unit, the calculator also estimates total construction or renovation costs, ensuring you stay within your budget.

While the primary unit of measurement is square feet (sq ft), the tool automatically converts and displays your results in square inches, square yards, square meters, and acres for ultimate convenience.

Application Instructions

Using our area and cost estimator is simple and intuitive. Follow these steps for accurate results:

First, select your desired geometric shape from the drop-down menu at the top of the calculator. Next, enter your measurements into the corresponding fields and select the appropriate unit of measurement for each value. Then, enter the quantity. For instance, if you are measuring two identical rooms, input the dimensions for one room and type "2" in the "Quantity" field. The tool will automatically multiply the result, giving you the total surface area for both spaces.

If you only need the area measurement, simply skip the "Optional cost calculation" section and click "Calculate." The tool will instantly display your shape's square footage and surface area across multiple units.

To estimate project expenses—such as the cost of installing tile or hardwood flooring—enter the price per square unit of your chosen material. The calculator supports cost calculations based on square inches, square feet, square yards, and square meters. Once you hit "Calculate," you will receive both the total surface area and the estimated material cost required to cover that area.

Important notes about the units

The calculator processes one unit of measurement at a time per input field. If you need to manually convert inches to feet, simply divide the inch value by 12.

For example, if your measured length is 5 ft 3 in, you should input it as 5.25 ft (since 3 in = 3/12 ft = 1/4 ft = 0.25 ft).

Alternatively, you can enter the entire value in inches. A length of 5 ft 3 in equals 63 in (since 5 ft × 12 in = 60 in, plus the remaining 3 in).

The same logic applies to the metric system. If you measure a length of 3 m 60 cm, you can input the value as either 3.6 m or 360 cm.

While the calculator's primary units are feet and square feet, it seamlessly accepts inputs in inches, feet, yards, millimeters, centimeters, and meters. Please note that to convert millimeters to feet, the value is divided by 304.8 (meaning 1 mm = 0.00328084 ft). If the inputted millimeter values are exceptionally small, the calculator may not be able to generate a result, as the converted footage will be too close to zero.

Unit conversion rules

Our square footage calculator relies on the following standard unit conversion rules:

• Square feet to square inches: multiply the value in square feet by 144 to get the value in square inches. To convert square inches to square feet, divide the value in square inches by 144.
• Square feet to square yards: divide the value in square feet by 9 to get the value in square yards.
• Square feet to square meters: divide the value in square feet by 10.764 to get the value in square meters.
• Square feet to acre: divide the value in square feet by 43,560 to get the value in an acre.

Area shapes and formulas

Understanding how to calculate square footage manually can be highly useful. Below are the mathematical formulas for all the geometric shapes featured in our tool. In every formula, A represents the total area (square footage), while the other variables are defined under each specific shape.

Square

Let the side length be a. Then,

$$A = a^2$$

Rectangle

Let a be the length and b be the width. Then,

$$A = a × b$$

Rectangle border

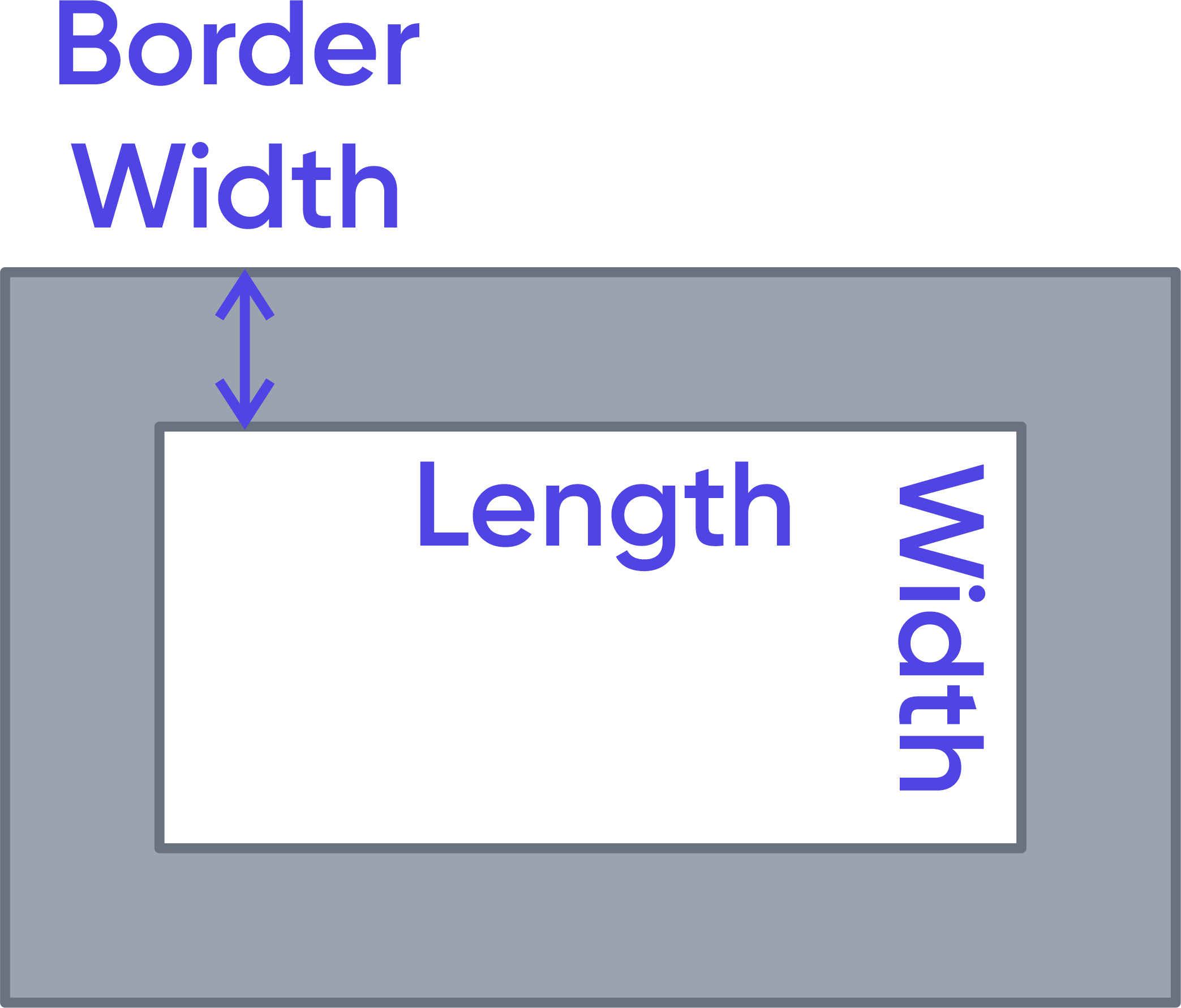
Let a represent the inner length, b represent the inner width, and c represent the border width. The square footage of the border area can be calculated by finding the difference between the total area and the inner area:

$$Inner\ Area=A_1=a×b$$

$$Total\ Area=A_2=(a+2c)(b+2c)$$

$$A=A_2-A_1$$

Circle

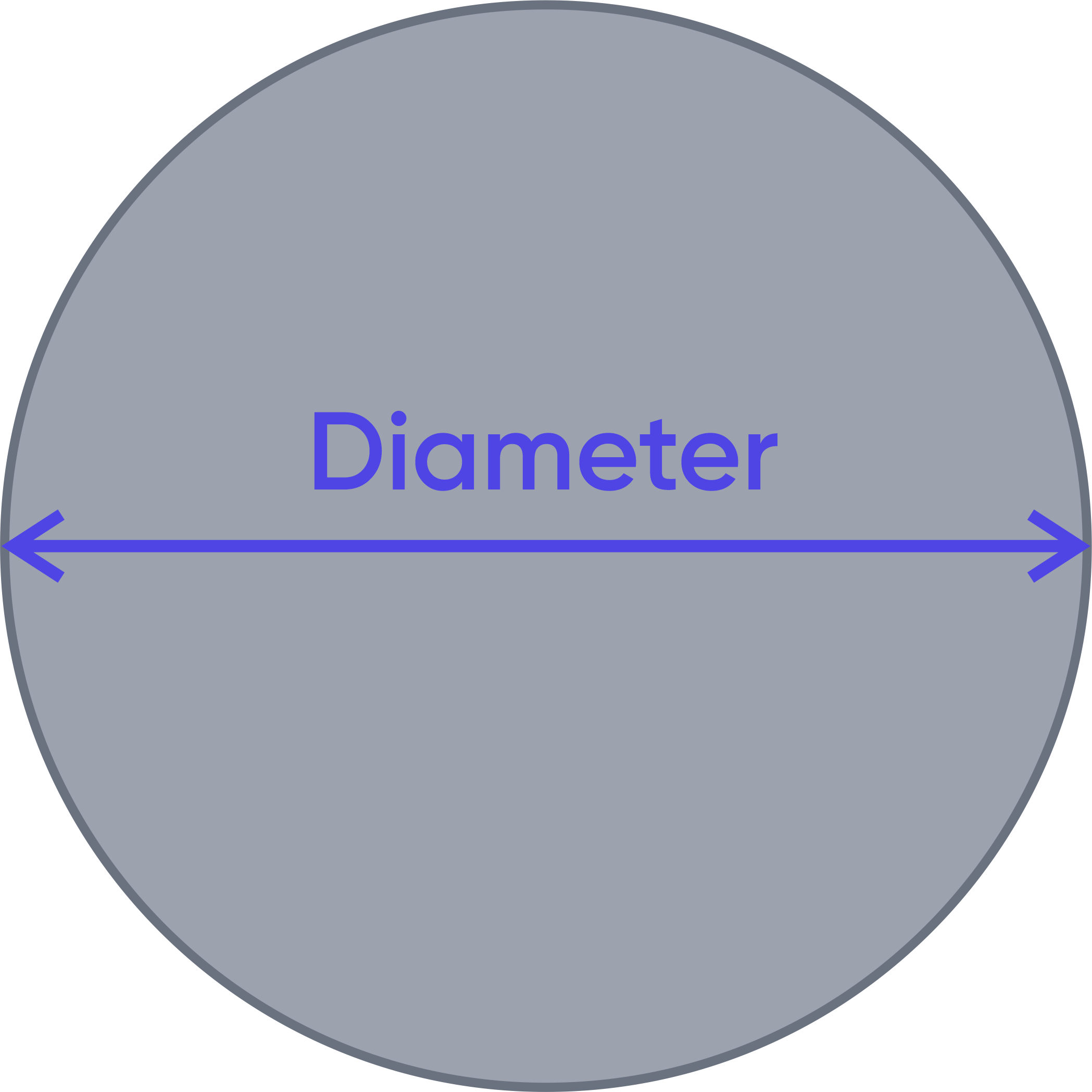
Let the diameter equal d and the radius equal r. Then,

$$A=π\frac{d^2}{4}$$

or

$$A=π r^2$$

Circle Border

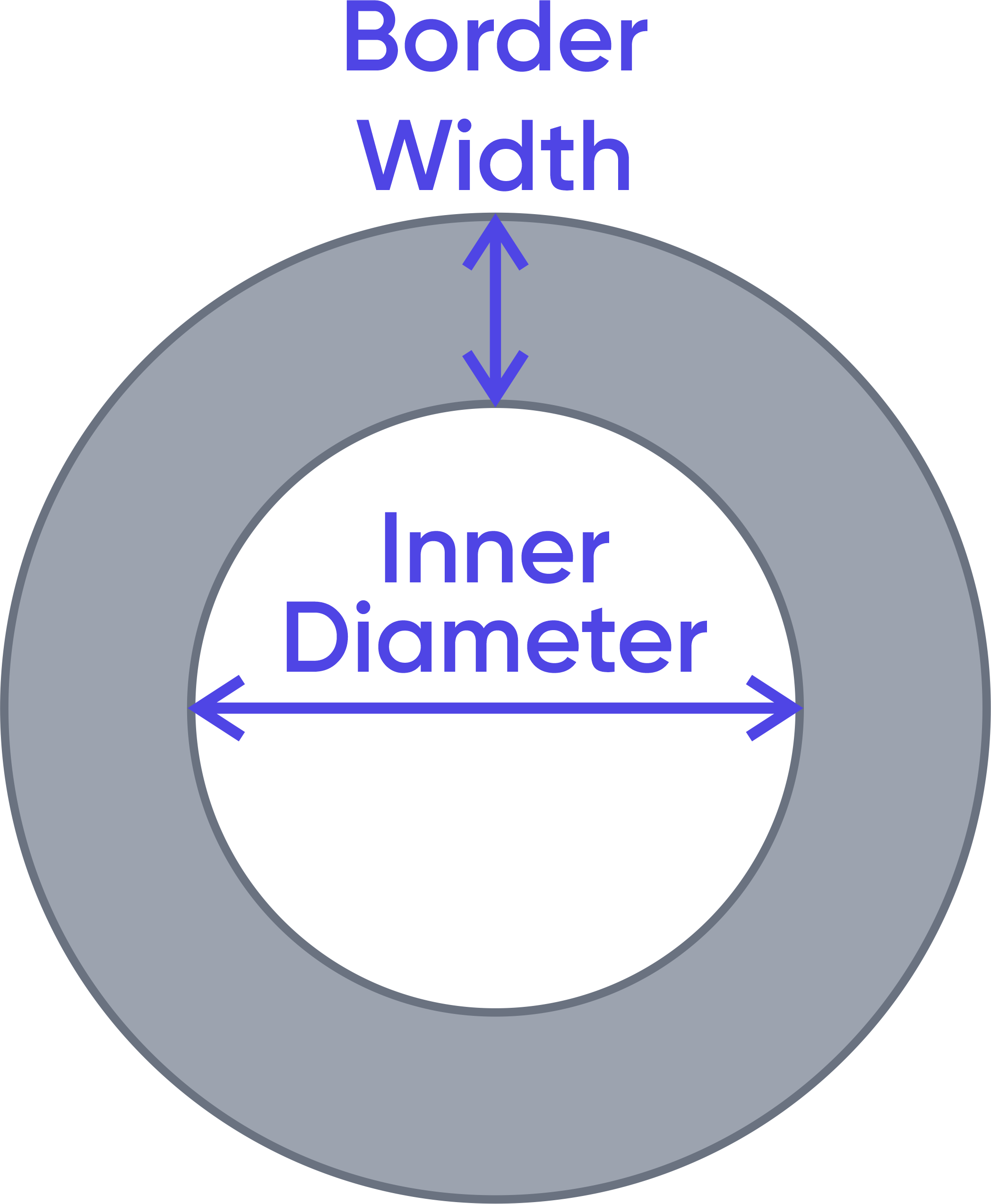
Let dᵢ represent the inner diameter, dₒ represent the outer diameter, and c represent the border width. This calculation assumes that only the inner diameter dᵢ and the border width c are known. The square footage of the border area is the difference between the area of the outer circle and the area of the inner circle. We can find the outer diameter as follows:

$$d_o=d_i+2c$$

Therefore,

$$Inner\ Area=A_1=π\frac{{d_i}^2}{4}$$

$$Outer\ Area=A_2=π\frac{{d_o}^2}{4}$$

$$A=A_2-A_1$$

Annulus

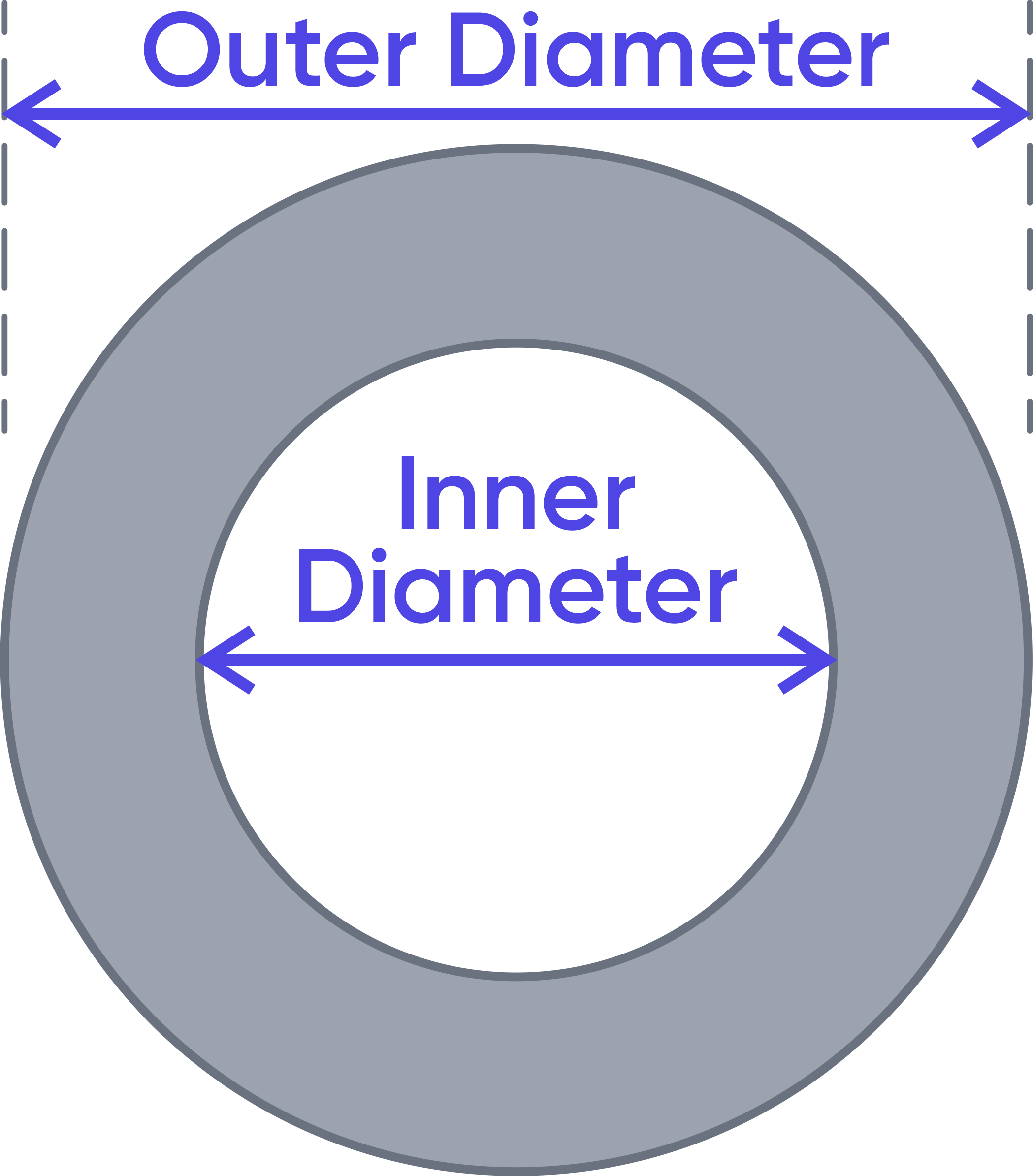
An annulus is essentially the same shape as a circle border. However, in this calculation, we assume that both the inner diameter dᵢ and the outer diameter dₒ are already known. Using the same logic as the previous shape:

$$Inner\ Area=A_1=π\frac{{d_i}^2}{4}$$

$$Outer\ Area=A_2=π\frac{{d_o}^2}{4}$$

$$A=A_2-A_1$$

Triangle

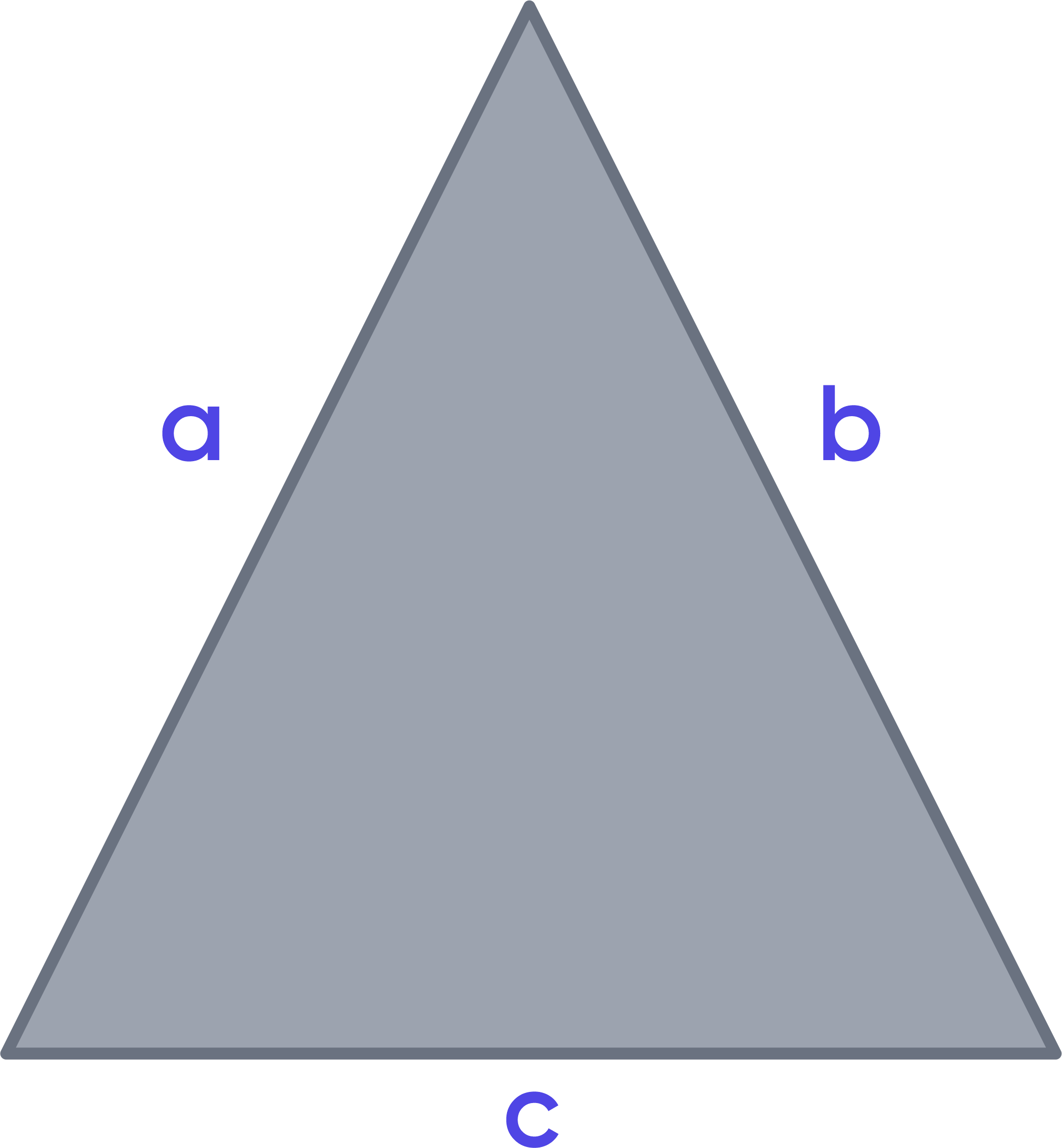
Let the sides of the triangle be a, b, and c. Using Heron's formula, the area of this triangle can be found as follows:

$$A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$$

where s is the semi-perimeter:

$$s=\frac{a+b+c}{2}$$

Trapezoid

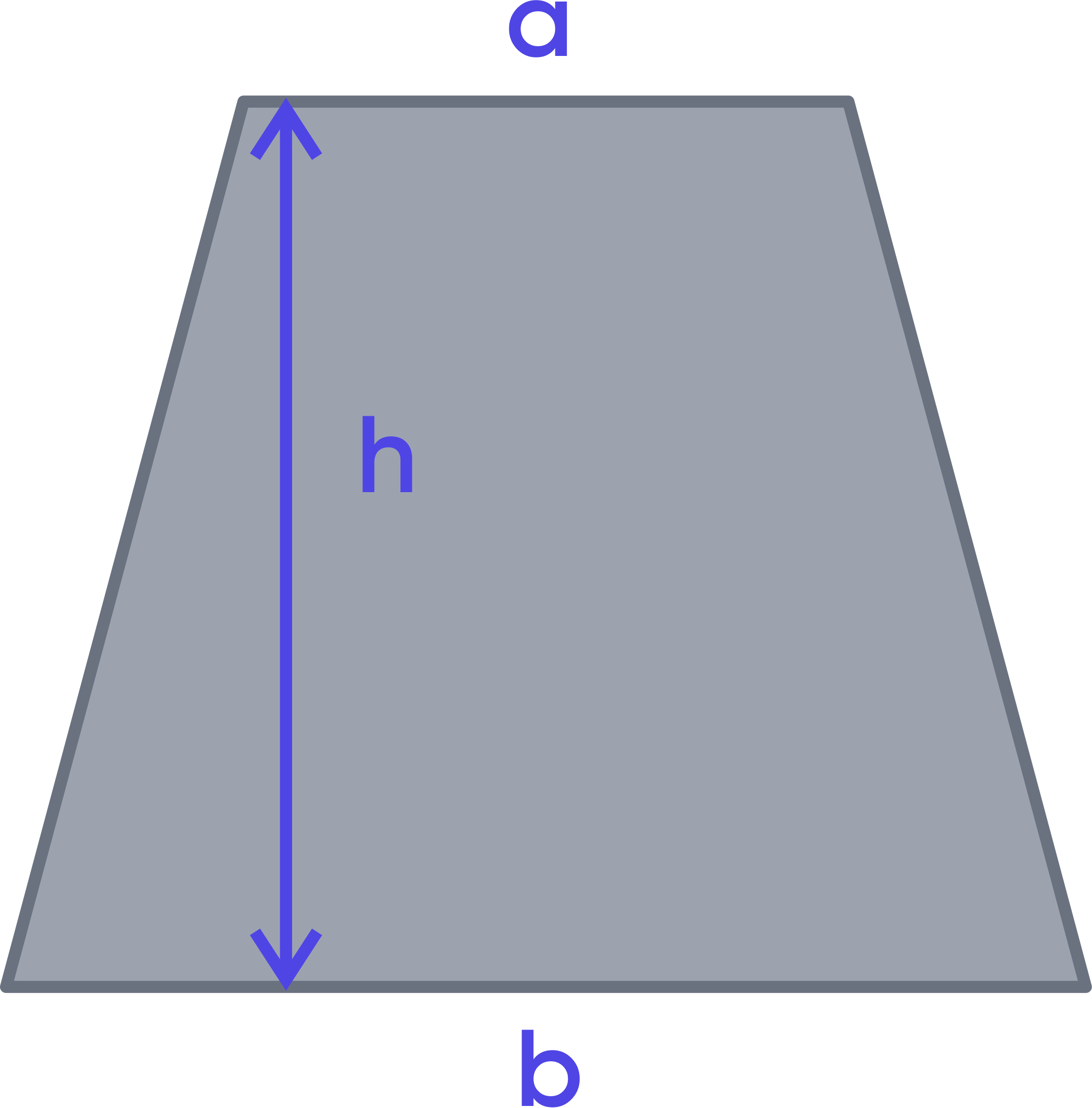
Let the parallel bases of a trapezoid be a and b, and its altitude (height) be h. Then the area of the trapezoid can be found as follows:

$$A=\frac{a+b}{2}× h$$

Practical example

Let's look at a real-world scenario. Suppose you need to find the square footage of a rectangular room to calculate the cost of installing new wooden floor tiles. First, measure the room's length and width. Let's assume the length is 15 feet, and the width is 9 feet. You also know that the wooden tiles you want to purchase are priced at $8 per square foot.

To estimate your total project cost, first select "Rectangle" from the area shapes drop-down menu. Next, input the values Length = 15 and Width = 9, ensuring you set the corresponding units to "ft" for both fields. Because you are only flooring a single room, leave the quantity at 1. Finally, enter the material price of $8 into the relevant field under "Optional Cost Calculation."

Once you press "Calculate," the tool instantly generates the following results:

• square footage = 135 ft²,
• square inches = 19,440 in²,
• square yards = 15 yd²,
• square meters = 12.54 m²,
• acres = 0.00310 acre,
• cost = $ 1,080.